回帰分析 とは？

回帰分析の特徴

回帰分析とは、関数をデータに当てはめることで変数の因果関係を証明し、結果の説明をしたり予測を行ったりすることです。ここでは回帰分析のメリットデメリットや活用についてご紹介します。

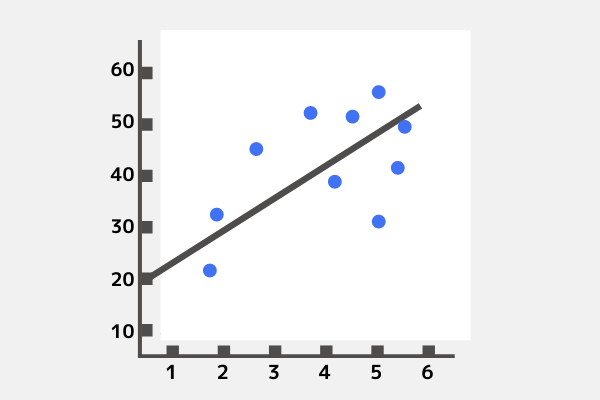
次のグラフは、家族の人数と、商品の購入量の関係を表したものです。10個の点は世帯を表しています。真ん中の直線が右上がりに引かれていることから、家族の人数が多くなるとその商品の購入量も上がるということが、このグラフから読み取れます。この直線は「回帰直線」と呼ばれています。

ここでは回帰分析のメリットデメリットや活用についてご紹介します。

回帰直線の求め方

「回帰直線」は、横軸をXとし、縦軸をYとしたグラフ上で「y=a+bx」の1次方程式で表わします。aは「回帰定数」と呼ばれ、「回帰直線」とYとの交点で、yの大きさを表わす値です。bは「回帰係数」と呼ばれ、「回帰直線」の傾きを表します。bの値がマイナスの場合、「回帰直線」は右下がりになります。

 

先ほどの例を使うと、家族の人数が横軸のxになり「説明変数」、そして購入量は縦軸のyで「目的変数」と呼ばれます。このように「説明変数」が一つの場合は、「線形単回帰分析」ともよばれます。他の「説明変数」を加えることも可能で、数式は「y=a+b1x1+b2x2」となります。「説明変数」が2個以上ある場合、「重回帰分析」と呼ばれます。「線形単回帰分析」よりも、より深い分析が可能です。このように関数をデータに応用することにより、ある変数の変動を別の変数の変動により予測することができます。

 

「回帰分析」のメリットとデメリット

「回帰分析」のメリットは、数式を用いた分析方法なので、単なる予測ではなく、根拠のある分析結果が得られることでしょう。数式に当てはめれば、手元にデータがなくても予測が可能です。またグラフに表すことで、見やすく簡単に理解できるので、情報共有がしやすくなります。デメリットとしては、剰余変数の存在を見逃してしまうと、誤った分析結果が出てしまうことでしょう。また「線形単回帰分析」のみでの分析が可能なデータは少なく、「重回帰分析」をしっかりと理解し、活用する必要があるということです。データ分析に関しては、エクセルなどのソフトウェアを活用すれば難しいことはないので、データの見極め、適切な推論をする能力が求められます。

 

混同しやすい「相関関係」と「因果関係」とは？

また、「回帰分析」を理解する上で必要な知識である「相関関係」と「因果関係」についても理解をしておきましょう。「相関関係」とは、文字のごとく、一方の値が変化するともう一方の値も変化する関係のことです。Aが増加するとき、Bも増加もしくは減少します。互いに相関しているため、Aを原因としてBが変動する、という関係が２つの値の間にはありません。つまり、疑似相関の関係である可能性もあります。AとBが別の要因によって起こっているのに、AとBの間に因果関係があるように見える関係を疑似相関と言います。相関係数は一般的に r であらわされ、-1≦r≦1の範囲をとります。0は相関がないことを表し、0より-1、1に近い値であるほど強い相関があることが示されています。「因果関係」とは、Aを原因としてBが変動する関係のことです。原因があり、そこから生ずる結果が存在する関係性です。データの読み間違いは「相関関係」と「因果関係」を混同してしまうと、データを正しく読み取れないので、しっかりと違いを理解しておきましょう。

 

回帰分析を理解し、マーケティングの予測に役立てよう

アンケート結果や、閲覧データなど、膨大なデータから顧客の行動を「予測」するのがマーケティングの重要な役割です。正しくデータを分析し、ユーザーやターゲット層、または商品やサービスについての理解が深まることにより、データをマーケティングに活かすことができるのです。数ある分析方法の中でも、「回帰分析」は、データ分析による予測の基礎と言えるでしょう。回帰分析をしっかりと理解し、マーケティングに活かしていきましょう。

コラム一覧へ戻る